 |
|
|||
|
Hyperbolic Space online exhibit - Introduction Model galleries Press and other resources |
Hyperbolic
Space |
|||
| In 1997 Cornell University mathematician Daina Taimina finally worked out how to make a physical model of hyperbolic space that allows us to feel, and to tactilely explore, the properties of this unique geometry. The method she used was crochet. Dr Taimina’s inspiration was based on a suggestion that had been put forward in the 1970’s by the geometer William Thurston (also now at Cornell). Noting that one of the qualities of hyperbolic space is that as you move away from a point the space around it expands exponentially, Thurston designed a paper model made up of thin cresent-shaped annuli taped together. But Thurston’s model is difficult to make, hard to handle, and inherently fragile. Taimina intuited that the essence of this construction could be implemented with knitting or crochet simply by increasing the number of stitches in each row. As you increase, the surface naturally begins to ruffle and crenellate. Taimina, who grew up in Latvia with a childhood steeped in feminine handicrafts, immediately set about making a model. At first she tried knitting - and you can indeed knit hyperbolic surfaces - but the large number of stitches on the needles quickly becomes unmanageable and Taimina realized that crochet offered the better approach. |
||||
 |
||||
| Crochet model of hyperbolic plane by Daina Taimina | ||||
The beauty of Taimina’s method is that many of the intrinsic properties of hyperbolic space now become visible to the eye and can be directly experienced by playing with the models. Geodesics – or straight lines – on the hyperbolic surface can be sewn onto the crochet texture for easy examination. Through the yellow lines in the model below look curved, folding along them demonstrably produces a clean straight line. |
||||
 |
||||
| Crochet hyperbolic plane with geodesics – straight lines – stitched on. | ||||
Likewise one can see immediately how the parallel postulate is violated. In the model below there are three straight lines that pass through a point external to a given line (the one at the bottom). All three of the upper lines never intersect the original line. With this physical model in your hands you can fold along each line and verify the untruth of Euclid’s fifth axiom yourself. The power of Taimina’s models resides in bringing abstract mathematics into the realm of tactile experience. |
||||
 |
||||
| Crochet model demonstrating the falsity of the parallel postulate. | ||||
| Another aspect of hyperbolic space that can be experienced with Taimina’s models is the properties of triangles. In school we learn that the angles of a triangle always sum to 180Ú. That is true on a Euclidean plane, but it is not true on a sphere or on a hyperbolic plane. On a sphere, the interior angles of a triangle always sum to more than 180Ú (a fact the reader may verify for themselves by drawing on a beach ball or balloon). On a hyperbolic surface the angles of a triangle add to less than 180Ú. Moreover, the larger triangle the smaller the angles will be. Until finally when the triangle points are infinitely far apart - making the largest triangle possible - the angles will sum to zero degrees! This Ideal Triangle and its angular oddity can be seen on the model below: | ||||
 |
||||
| Crochet model showing an Ideal Triangle, whose angles sum to zero degrees. | ||||
Taimina’s crochet models also enable us to make more exotic hyperbolic constructions. Just as we can take a piece of ordinary paper and wrap it into a cone, so we can make a hyperbolic cone from a piece of hyperbolic paper. The resulting form is known as a pseudosphere. Crochet model of pseudosphere – the hyperbolic equivalent of a cone. |
||||
 |
||||
| Here is the rate of increase is one stitch in every three. | ||||
 |
||||
| Here we are increasing one stitch in every two. | ||||
 |
||||
| And here, we are increasing in every stitch. | ||||
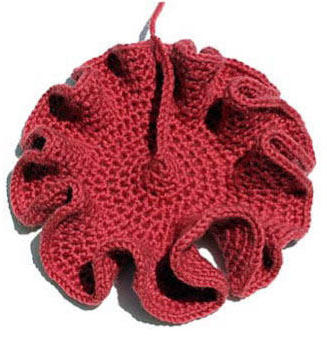
| As the rate of increase of the stitches increases, the construction becomes increasingly crenellated. In effect the space around any point expands ever more exponentially. Whereas all spheres have the same form - varying only in size - hyperbolic surfaces may differ dramatically from an external point of view. Mathematically speaking, we characterize this quality by the radius of the hyperbolic plane: the more crenellated the surface appears, the smaller its radius; the flatter the surface, the greater its radius. A regular Euclidean plane can be understood as a hyperbolic plane of infinite radius. The radius of any given hyperbolic plane is the radius of a circle that would sit flatly on an a tabletop. | ||||
 |
||||
| Measuring the radius of a hyperbolic surface. | ||||
| In the series of pseudospheres above, the radii get progressively smaller, leading to ever more crenellated models. By using a high rate of expansion - by increasing in every stitch, or even increasing two or three times in every stitch - we can make a hyperbolic surface that starts off from just a few stitches and expands out to an arbitrarily long perimeter. Dr Taimina’s personal record is a plane that began with two dozen stitches and has a perimeter length of 369 inches. The width of this model is just 4 inches and the total weight of wool is nearly a pound. Dr Taimina’s models are featured in the Smithsonian's collection of American Mathematical Models. | ||||
| [ next ] | ||||
| © 2003–2018 The Institute For Figuring | ||||